표현론적ㆍ해석학적ㆍ기하학적 방법으로 수론 연구
3요소 사이의 랭글란즈 대응, 아직 미해결로 남아있어
수학의 주요 연구분야이자 정수론의 핵심이론인 ‘보형 형식과 갈루아 표현법’을 주제로 개최된 제 2회 포스텍 일주수학학교가 7월 중순부터 개최되어 2주 동안 진행되었다. 총 40개의 강의와 10개의 세션으로 구성된 일주수학학교는 앞으로 세계 수학계를 이끌 젊은 수학자들이 그동안 매진해온 연구를 국내외 연구자들과 대학원생들에게 구체적으로 설명하는 자리를 갖는 좋은 기회가 되었다.
정수론의 핵심이론이라 불리는 ‘보형 형식과 갈루아 표현법’이란 무엇일까. 이번 일주수학학교에 참석한 강사진 중 한 명인 우리대학 박지훈(수학) 교수를 찾았다.
정수론을 공부하는 수학자들이 관심을 가지는 것은 수의 의미와 구조에 대한 연구일 것이다. 우리들이 어릴 적부터 보아온 0,-1,1,-2, 2-3,3,,... 같은 정수에 대한 연구 (예를 들면 소수에 관한 연구)부터 시작해서 유리수체 (정수들의 비로 나타나는 수의 모임)에 관한 연구 등이 이에 포함된다. 좀 더 나아가면 유리수를 계수로 가지는 모든 유한다항식의 해집합들을 모아두게 되면 수체(field)를 이루는데, 이런 수체의 원소를 대수적 수(algebraic numbers)라고 부른다. 물론 수 중에 대수적 수가 아닌 수도 존재하며 이런 수들은 초월수(transcendendal numbers)라고 한다. 예를 들면 원주율 pi와 자연 상수 e등이 초월수임이 증명되어 있다. 아쉽게도 초월수의 집합은 체의 구조를 가지지 못하여(덧셈에 대해 닫혀있지 않다) 그 연구를 더 어렵게 만든다. 초월수에 대해서도 좋은 수학적 이론이 많지만 이번 기고문에서는 대수적 수체 (algebraic number field)를 공부하는 현대정수론의 핵심이론에 대해 알아보도록 하겠다.
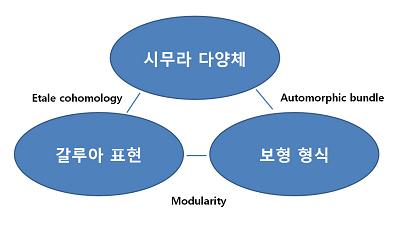
대수적 수체를 공부한다는 의미가 무엇일까? 여기에는 다양한 답이 존재한다. 학부대수학의 용어를 빌리자면 bar{Q}를 이해하는 것인데 bar{Q}는 Q의 복소수체 안에서의 유한 확장체 K들(number field라 부르자)의 합집합이다. 유리수체(Q)안에 정수환(Z)이 있듯이, K안에도 O_K라고 부르는 정수환이 존재하고, O_K의 산술적 구조를 공부하고 싶어 한다. O_K안에서 이데알(ideal)이 어떻게 기약 이데알(prime ideal)로 분해되고, 이데알이 언제 한 원소에 의해 생성되는지 등이 굉장히 중요한 문제이다. 놀라운 사실은 이렇게 산술적인 문제를 풀어가는 과정에 굉장히 다른 분야의 수학을 크게 이용한다는 사실이다. 기고문의 제목인 갈루아 표현, 보형 형식, 그리고 시무라 다양체는 위와 같은 산술적인 문제에 각각 군의 표현론적 방법, 해석학적 방법, 그리고 기하학적인 방법을 이용할 수 있음을 나타내고 있다. 차례대로 어떻게 위한 같은 표현론적, 해석학적, 그리고 기하학적 방법이 수론의 문제에 이용될 수 있는지 알아보도록 하자.
먼저 number field K의 산술을 공부하기 위한 방법으로 갈루아 이론(Galois theory)이 있다. 학부대수학의 꽃이라고 할 수 있는 5차이상 Q상의 대수방정식이 일반적으로 근의 공식을 가지지 않는다는 아벨과 갈루아의 정리는 수체의 산술적 정보를 갈루아 군(Galois group)에 대한 정보로 바꾸어 이해하는데서 오는 대표적인 결과물이다. 좀 더 구체적으로 5차 다항식 f(x) in Q[X]에 의해 주어지는 갈루아 확장체를 K라고 하고, K에서 K로 가는 동형사상으로 정의되는(갈루아 군이라 부른다) Gal(K/Q)이 S_5와 동형(isomorphic)이라고 하자. 그러면 n이 5이상 일 때 대칭군 S_n이 증명가능하지 않다는 군의 정리를 갈루아 이론을 통해 체의 산술에 대한 정리로 바꾸면 정확히 f(x)가 근의 공식을 가지지 않는다로 생각될 수 있다. 즉 K와 bar{Q}를 공부하는 좋은 방법 중 하나가 갈루아 군 Gal(K/Q)과 Gal(bar{Q}/Q)을 공부하는 것이다. 그러면 자연스러운 질문이 갈루아 군은 우리가 어느 정도 이해하고 있는가이다.
갈루아 군(Galois group), 일반적으로 군을 공부하는 대표적인 방법으로 그 군의 표현론이 있다. 즉 선형대수학을 힘을 빌어 군을 공부하고자 하는 것이다. 조금 더 구체적으로 갈루아 군이 작용하는 차원 n인 선형공간을 많이 찾을 수 있다면, 갈루아 군에서 행렬 군으로 가는 동형사상을 가지게 된다. 이러한 동형사상을 갈루아 군의 표현이라고 부른다. 여러 가지 군중에서도 수학자들이 가장 잘 이해하는 군이 행렬 군이므로 갈루아 군에서 행렬 군으로 가는 함수, 즉 갈루아 표현이 존재한다면 갈루아 군의 성질을 이해하는데 많은 도움이 될 것이다. 대수적 수체의 문제를 갈루아 군의 표현 (줄여서 갈루아 표현)의 문제로 바꿔 놓고 나면 그 다음의 물음은 갈루아 표현의 존재에 관한 문제가 될 것이다.
의미 있는 연구가 가능한 갈루아 표현의 존재를 증명하는 과정에서 위에 언급한 해석학적 존재인 보형 형식과 기하학적인 존재인 시무라 다양체가 큰 역할을 한다. 우선 갈루아 표현과 보형 형식의 관계부터 살펴보도록 하자. 보형 형식은 포앙카레 상반면에서 정의된 해석적(holomorphic) 함수들 중에 특정 변환공식을 만족하는 함수들을 말한다. 정의 자체가 복소 해석학적으로 주어져 있지만, 보형 형식의 특징은 복소 해석학적 정의와 동일한 기하학적 대수학적 정의가 존재한다는 사실이다. 이 같은 사실들에 기반에 두고 시무라, 아이흘러, 들린느 그리고 세르 같은 유명 수학자들이 보형 형식이 주어지면 그에 대응하는 갈루아 군의 표현을 만들 수 있음을 보였다. 역으로 특정 갈루아 표현이 존재하면 거기에 대응하는 보형 형식이 존재하는가 하는 질문을 할 수 있는데, 수학 역사적으로 유명한 와일즈(Wiles)의 페르마의 대정리 증명 과정에서 이 질문이 굉장히 중요한 역할을 한다. 부연 설명하면 와일즈는 위 질문의 특정한 케이스인 “타원 곡선에 주어진 갈루아 표현은 보형 형식으로부터 온다”는 타니야마-시무라 추론(Taniyama-Shimura conjecture)의 일부를 증명함으로써 페르마 대정리를 유도해 낼 수 있었다. 특정한 다항식의 해의 존재 유무를 갈루아 표현(대수적 존재)과 보형 형식(해석적 존재)의 관계를 이해함으로써 가려낸 것이다. 이러한 대응은 좀 더 일반적으로 확장 될 수 있는데, 그러한 대응을 수학자들은 랭글란즈(Langlands)라는 수학자의 이름을 따서 랭글란즈 대응라고 부른다.
이제 시무라 다양체의 이야기를 해보자. 어떻게 갈루아 표현과 기하학적 대상을 연결시킬 수 있을까? 20세기 최고의 대수기하학자라고 일컬어지는 그로쎈딕(Grothendieck)은 에딸 코호몰로지(etale cohomology) 이론을 도입함으로써 임의의 대수적 수체위에 정의된 대수적 다양체가 주어지면 갈루아 표현을 줄 수 있음을 증명했다. 정수론(갈루아 표현)과 대수기하(대수 다양체)의 연결이 그로쎈딕에 의해 주어진 것이다. 다양체의 여러 성질들이 갈루아 표현의 성질들로 바꾸어 이해될 수 있고, 그 반대로 갈루아 표현의 특징이 대수 다양체에 투영되기도 한다. 그리고 다양한 대수 다양체 중에서도 그에 대응되는 갈루아 표현이 보형 형식과 자연스럽게 연결되는 다양체가 존재하는데, 이를 시무라 다양체라고 한다. 예를 들면 포앙카레 상반면을 행렬 군으로 자른 대칭공간은 모듈러 곡선(modular curve)이라 불리는 시무라 다양체다. 모듈러 곡선의 에딸 코호몰로지, 즉 갈루아 표현과 그 위에 정의된 보형 형식이 랭글란즈 대응을 이루는 것이다. 이 대응을 통해 정수론의 많은 문제들이 해석하적 기하학적으로 연구되고, 역으로 정수론의 지식을 통해 해석학과 대수 기하학의 문제를 풀기도 한다.
갈루아 표현, 보형 형식, 시무라 다양체, 그리고 이들 사이의 랭글란즈 대응은 현대 수학의 중요한 연구 주제로 아직도 많은 부분 미해결로 남아 프로 수학자들과 미래에 정수론과 산술기하를 전공할 포스텍의 젊은 예비 수학자들의 도전을 기다리고 있다. 포스텍 학생들이 수학에 큰 꿈을 가지시고 즐거운 수학(즐수)하시길 바란다.


