‘암호’, ‘보안’ 이라고 하면 국가 정보원 또는 산업스파이들의 활동 등을 연상하게 된다. 영화 ‘뷰티플 마인드’에서 주인공 내쉬는 러시아 정부가 신문, 잡지 등을 통하여 첩보원들에게 보내는 비밀 메시지를 알아내려고 했다. 첩보원들은 메시지를 읽는 방법(암호를 푸는 key)을 알고 있고, 주인공 내쉬는 기사의 패턴을 통하여 그 암호를 풀려고 한 것이다. 이 방식은 고전 암호 기법으로 ‘대칭키 암호 방식’이라고도 한다. 즉, 송수신자 사이에 메시지 전달 방식(암호 key)을 공유한 후 비밀 메시지를 보내는 방법으로. 이 대칭키 암호 방식은 키를 공유하고 비밀 유지나 변경 등에 많은 자본과 노력이 필요하기 때문에 군사, 국가정보 차원에서 주로 사용되었던 것이다.
그러나 컴퓨터, 네트워크, 무선기술 발전에 힘입어 우리의 일상생활의 범위가 디지털 통신을 통하여 전 세계로 확대되었다. 초기에는 e-mail이나 문서 전송이 인터넷 사용의 주요 목적이었으나 점점 사이버 쇼핑, 인터넷 뱅킹 등 개인의 정보 보호, 메시지의 보호 등이 요구되는 서비스가 급증하고 있다. 인터넷 상에서 이러한 서비스들을 안전하게 제공하기 위해 해결해야 할 문제들은 다음과 같다. A로부터의 편지를 받고 B는,
1.다른 사람이 내용을 보지 않았는 가? (기밀)
2.편지의 내용이 변조되지 않았는가? (변조)
3. A가 보낸 것은 확실한가? (위장)
4.A가 보낸 사실을 부인하지 않을까? (송(수)신 부인)
를 염려하게 된다. 대칭키 암호는 A와 B가 같은 키를 갖기 때문에 전송된 편지가 정말로 A가 만든 비밀메시지인지 B가 만든 것인지 구별할 수 없으며 이 때문에 A가 보낸 사실을 부인할 수도 있게 된다.
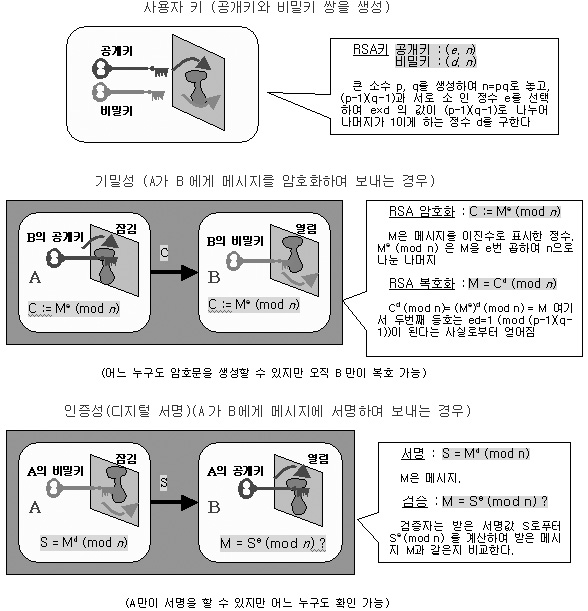
현대의 암호학 - 공개키 암호시스템
현대의 암호를 ‘공개키 암호시스템’이라고 한마디로 표현할 수 있는데, 이는 사용자가 모든 사람에게 공개하는 공개키(public key)와 자신만이 갖는 비밀키(private key) 쌍을 키로 갖는 시스템이기 때문이다.
A가 B에게 비밀 메시지를 보내려고 할 때 B의 공개키를 얻어서 암호화한 암호문을 B에게 보내면 B는 자신만이 갖는 비밀키로 복호를 한다(기밀성). A가 서명과 함께 B에게 메시지를 보내려고 할 때 A의 비밀키로 암호화 한 암호문(서명값)과 메시지를 B에게 보내면 B는 A의 공개키로 복호를 하여 얻은 메시지와 받은 메시지가 일치하는지를 확인함으로써 그 메시지가 A로부터 왔으며 변경되지 않았음을 확인할 수 있다(변조 및 위장 방지). 그리고 A와 B 사이에 분쟁이 발생했을 경우 B는 A로부터 받은 메시지와 서명을 판사에게 보여주면 판사가 A의 공개키로 확인해 볼 수 있고 A만이 그 서명을 만든 비밀키를 가지므로 A는 그 메시지에 대한 책임을 지게 된다(부인 방지). 아래의 그림에 공개키 암호의 기본 흐름을 가장 널리 알려진 RSA(Rivest, Shamir, Adleman이 발표. 1978)를 예로 도시하였다.
공개키 암호 시스템의 안전성은 공개된 정보로부터 비밀 정보를 어느 정도의 어려움으로 얻을 수 있느냐이다. RSA 시스템에서는 공개키(e, n)로부터 비밀키 d를 구할 수 있는가의 문제이다. 만약 p, q를 알 수 있으면 A가 d를 계산한 방법으로(수학적으로 아주 간단한 알고리즘이 있음) 비밀키를 알아낼 수 있다. 따라서, n으로부터 p, q를 구하는 인수분해문제를 풀면 모든 RSA 키를 알아낼 수 있는 것이다. 주어진 정수 n을 인수분해 하는 방법은 누구나 알고 있다. 그러나 정수의 크기가 커지면 시간이 아주 많이 걸린다. 개인 사용자들의 공개키는 현재 1024비트(십진수로 약 300자리수)키를 사용하는데, 알려진 가장 빠른 소인수 분해 알고리즘을 사용하고 슈퍼컴퓨터로 계산을 한다 하더라도 지구 역사 정도의 시간이 지난 후에나 답을 얻을 수 있다. 최근 Daniel Bernstein(University of Illinois, 수학 교수)는 1024비트 키의 안전성에 관한 위협적인 결과를 발표하였다. 10만 달러의 비용이 있으면 현재 모든 은행의 개인 인터넷뱅킹 사용자들의 비밀키를 수십초 또는 수분 내에 알아낼 수 있다는 것이다. 전문가들은 Bernstein의 알고리즘이 구현이 어렵기 때문에 적어도 2009년까지는 안전한 것으로 보고 있다. RSA 연구소 홈페이지(http://www.rsasecurity.com/rsalabs/) 에서 RSA 소수 들에 대한 최근 소식들을 알 수 있으며 RSA-challenge 프로그램도 있다.
상용화된 암호시스템 중 키가 가장 짧은 것은 타원곡선 암호 시스템(ECC)으로 160비트(약 55자리수: RSA의 약 1/6) 키를 사용하도록 권장하고 있으며 무선 인터넷에서 사용되고 있다. 이 암호시스템은 타원곡선 군에서의 이산대수 문제의 어려움을 이용하며 그 어려움의 정도가 소인수 분해 어려움에 비해 상당히 크다. 따라서, RSA 키의 크기 증가 속도를 기하급수적으로 늘어난다고 표현하면 타원곡선 암호의 키는 산술급수적으로 늘어난다고 할 수 있다.
생활의 일부분이 된 암호 사용
인터넷쇼핑, 인터넷뱅킹 등 전자상거래, 전자결제 등의 모든 보안 서비스들이 공개키 암호 시스템을 이용하고 있다.
“Auction은 VeriSign에서 인증하는 128Bit SSL 암호화 알고리즘을 이용하여 네트워크 상의 개인정보를 안전하게 전송할 수 있는 방식을 채택하고 있습니다.”
이 문장은 사이버 경매 사이트로 유명한 Auction의 <개인정보 보호 정책>에서 인용한 문구이다. VeriS ign은 미국의 공개키 인증기관이고, 128Bit은 메시지 암호에 사용된 대칭키의 크기, 그리고 SSL(Secure Sockets Layer)는 암호 알고리즘을 장착한 네트워크 프로토콜이다. 대칭키를 암호화 하기 위해 공개키 암호 방식 RSA를 사용하고 있다.
증권 거래시 공인인증서 사용자가 하반기에 100만명을 넘어설 것으로 예상하고 있고, 인터넷뱅킹시 공인인증서 사용자가 140만명 등 그 사용자가 급증하고 있다고 한다(전자신문 5월 3일 기사). 여기서 공인인증서라 함은 앞에서 설명한 정확한 공개키를 제공하기 위해 발행된 데이터를 일컫는다. 즉, 공개키 암호 시스템은 이제 우리 생활의 일부가 되어 가고 있는 것이다.
수학과 암호학
암호는 정보를 갖지 않으면 답을 알기 어려워야 하는 특성 때문에 암호학자들은 암호 체계의 디자인에 수학에서 아주 어렵다고 알려진 문제들을 적용해 보고자 노력한다. 소인수 분해 문제 이외에도 이산 대수(discrete log problem), 격자점 문제(lattice), 그리고 켤레 찾기(conjugate problem) 등이 현재까지 성공적으로 암호에 응용된 문제들이다. 수학에는 아직도 해결되지 않은 문제들이 엄청나게 많기 때문에 새로운 암호 시스템의 가능성은 무궁 무진하다.
새로운 암호 시스템을 디자인 하기 위해 적어도 다음 사항들을 고려해야 한다.
-암호학의 재료는 현대 컴퓨터의 특성상 0과 1을 나열한 비트 스트링이다. 수학의 재료는 ‘수’이다. 비트 스트링을 ‘수’로, ‘수’에서 비트스트링으로 변환할 수 있어야 하며 그 방법은 효율적이어야 한다.
-‘수’들 사이의 규칙은 계산이 아주 효율적이어야 한다. 스마트카드, 휴대폰 내의 아주 작은 하드웨어에서도 효율적으로 구현 가능해야 한다.
-규칙을 이용하여 암호화, 디지털 서명, 키 교환 등의 프로토콜을 제공할 수 있어야 한다.
-현존하는 공격 기술과 이론에 대하여 얼마나 안전한가에 대한 연구가 지속되어야 한다.
위의 문제들은 여전히 현존하는 암호 체계들에서도 연구되고 있다. 결국 수학적 도구와 매체를 도입하여 암호를 만들었기 때문에 위의 문제들을 해결하기 위해서도 수학적 이론들이 많이 발전해야 한다.
컴퓨팅 능력과 네트워크 속도의 증가로 기존 암호체계의 키 크기가 점점 커지고 있다. 현존하는 암호 체계는 적어도 1024비트 RSA 시스템의 안전도와 같도록 키 크기를 정하고 있지만, 이것도 몇 년 남지 않았다. 한편, 지난 90년대부터 양자적 특성을 이용해 전혀 새로운 컴퓨터가 연구되고 있다. 이 컴퓨터가 실용화되면 현존하는 모든 암호체계는 순식간에 무너질 것이다. (현존하는 컴퓨터로 약 300년이 걸려야 풀어내는 암호체계도 똑같은 속도로 돌아가는 양자컴퓨터는 4분 만에 해독할 수 있다)
컴퓨팅 파워의 증가와 양자컴퓨터의 개발 등은 새로운 체계의 암호 시스템을 요구하고 있다. 이는 수학의 어려운 문제들을 탐구해야 함을 의미한다. 암호이론과 기술은 다른 나라가 아무리 발전해도 우리만의 이론, 기술이 꼭 있어야 하는 분야이다. 결국 우리의 안전한 생활을 위해서 수학의 많은 문제들을 연구해야 할 필요가 있는 것이다.
저작권자 © 포항공대신문 무단전재 및 재배포 금지


