순수수학을 전공으로 하는 사람들은 그 학문의 응용보다는 단지 호기심과 재미로 연구하는 경우가 많다. 실례로 푸앵카레 추측을 풀어서 세계적으로 유명세를 탄 러시아 수학자 그리고리 페릴만(G. Perelman)은 필즈메달 수상을 거부했다. 또한 그 문제를 풀어서 클레이 재단으로부터 받게 되는 백만 달러의 상금도 거부했는데, 영국의 모 일간지와의 인터뷰에서 “나는 언론의 관심을 받을 만한 사람은 아니다.”라며 “수학을 좋아서 연구했을 뿐 상금에는 관심이 없다.”라고 말했다. 즉 호기심과 재미로 연구를 했는데, 굳이 돈이나 상을 받을 필요는 없다는 것이다.

글쓴이가 하는 연구 역시 순수수학의 한 분야인 조화해석학이다. 조화해석학은 함수의 특성을 파악하고, 그 함수의 푸리에 변환의 성질을 잘 파악하고 연구하는 학문이다. 글쓴이는 Lp공간이나 더 확장된 로렌츠(Lorentz) 공간에서의 함수를 주로 다룬다. Lp공간은 함수들의 집합인데 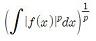                              의 값이 유한한 모든 함수를 모아 놓은 것이고, 로렌츠 공간은 Lp공간의 경계에 있어서 Lp공간에 안타깝게 들어가지 못한 함수를 포함한 조금 더 큰 공간이다. 특히 여러 문제를 다루는 데 있어서 큰 공간이 더 많은 함수를 가지고 있기 때문에 로렌츠 공간을 보편적으로 사용하고 있다.

조화해석학에서 글쓴이가 다루는 여러 문제들은 스타인(E. Stein)의 제한(Restriction) 문제에서 시작되었다고 볼 수 있다. 제한 문제는 원래 함수와 그 함수의 푸리에 변환 함수의 Lp노름(norm)의 크기를 비교하는 문제이다. Lp노름은 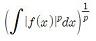                           의 값으로 정의한다. 이와 관련된 미해결 문제는 여러 가지가 있다. 그 중 유명한 한 가지 문제는 푸리에 변환한 함수의 정의역을 3차원 이상의 단위 구의 겉넓이로 제한(restriction)하고 Lp노름을 구하고 원래 함수의 Lp노름과 어떤 관련이 있는지를 알아보는 것이다. 정의역을 단위 구의 부피로 하지 않고 겉넓이로 하는 이유는 간단하다. 단위 구의 부피로 해서 계산을 하면 결과가 너무 쉽게 나오기 때문에 많은 흥미를 끌지는 못하지만, 겉넓이인 경우에는 아직까지도 완벽하게 다 풀리지 않았다.

이와 관련된 문제의 접근 방법 중 한 가지는 다음과 같다. 오직 L2노름에서만 함수와 푸리에 변환한 함수의 노름이 일치한다. 그래서 푸리에 변환한 함수의 적분 구간을 잘게 쪼개서 좋은 부분은 그대로 놓아두고 값이 좋지 않은 부분은 적분 구간을 더 잘게 쪼개서 계산을 한다. 그 다음, 이렇게 합한 값의 Lp노름과 원래 함수의 Lp노름을 비교한다. 이와 관련해서 반데르코프(Van der Corput) 보조정리를 이용한 푸리에 함수 값의 추정이 자주 사용된다. 이 보조정리는 주로 푸리에 함수와 이와 비슷한 함수를 부분적분을 이용해서 적분 값을 훨씬 더 빠르게 줄여나갈 수 있다는 스타인의 정리이다. 조화해석학에서 가장 기본적인 보조정리 중 하나이다.

조화해석학의 많은 문제들이 풀렸고, 안 풀린 문제들이 미해결문제로 남아 있다. 안 풀린 문제들은 지금까지 알려진 방법으로는 잘 해결되지 않기에 남겨져 있는데, 울프(T. Wolff)란 수학자가 응용수학의 한 분야인 조합론을 이용해서 지금까지 상당히 복잡한 문제를 훨씬 쉽게 접근할 수 있도록 했다. 특히 카케야(Kakeya) 집합(평면 상의 모든 방향으로 움직일 수 있는 단위 선분의 집합)의 바늘 문제에 관해서 탁월한 결과를 얻을 수 있게 되었다. 물론 울프뿐만 아니라 유명한 수학자 불갱(J. Bourgain)이나 크리스트(M. Christ)가 역시 조합적인 방법으로 문제에 접근하고 여러 방면으로 많은 결과를 내어 놓았다. 그래서 요즘은 한 분야의 문제를 해결하기 위해서 여러 다른 분야의 기술과 방법을 사용해 문제에 다각도로 접근하는 시도가 더욱 많아졌다.

글쓴이가 연구하고 있는 문제는 5차원에서 특수한 2차원 평면이 주어졌을 때 함수와 그 평면상에서만 적분한 함수 값들의 Lp노름을 비교하는 것이다. 그러기 위해서는 합성곱(convolution)의 개념을 이해해야 하는데, 합성곱이라는 것은 쉽게 이야기하면 두 함수가 있으면 두 함수의 적분 값의 평균 값을 구하는 역할을 하는 것이다. 그래서 2차원 평면과 함수를 합성곱을 한 후에 Lp노름을 구하고 원래 함수의 Lp노름을 구한다. 이 문제는 푸리에 변환을 이용해서 계산을 할 수 있으나, 크리스트의 조합적인 방법을 쓰면 전혀 다른 방법으로 계산을 할 수가 있다. 이 문제의 시초는 n차원 공간 상에서 특수한 곡선과 일반적인 함수의 합성곱의 Lp노름이 원래 함수의 적분 값의 Lp노름과 어떠한 관계가 있는지 알아보는 데 있다. 이 문제의 접근 방법은 우선 푸리에 함수를 사용하여 이 함수들을 중첩하는 데 있다. 푸리에 함수들을 중첩해서 적분하면 계산이 좀 더 수월해지고 조금 더 나은 환경에서 가능해진다. 또 다른 방법으로는 최근에 울프ㆍ크리스트 등이 사용한 조합적인 접근 방식이다. 조합적인 방법은 간단한 함수를 이용해서 그 함수가 정의된 영역을 새롭게 확장해나가면서 문제를 해결한다. 함수의 영역을 확장해나갈 때 조합적인 방법이 사용된다. 양쪽 다 각자의 장점들이 있다. 푸리에 함수를 중첩하는 방법은 주로 제한 문제에서 사용하기 좋고, 조합적인 방법을 사용해서 집합을 확장해나가는 방법은 합성곱 문제를 풀 때 사용하기 좋다.

그리고 글쓴이가 연구하는 문제도 n차원으로 확장해서 쉽게 생각은 할 수 있으나, 문제는 조금 더 복잡해지기 때문에 가장 쉬운 5차원에서 특수한 2차원 평면 문제를 다루고 있다. 물론 예상 범위에서 원하는 결과가 나왔는데, 그 영역의 마지막 한 점을 빼고는 증명이 되었다. 마지막 점은 좀 더 심화된 방법을 써서 해결해야 하기에 아직 연구 중에 있다. 그러면 자연스럽게 다음과 같은 질문을 할 수 있다. 만약 특수한 평면이 아니라 일반적인 평면을 가지고 문제에 접근하면 어떨까 하는 것이다. 문제는 함수 자체도 일반적인 Lp공간에서 가져오기 때문에 생각해야할 변수가 너무 많아진다. 평면 자체도 너무나 많은 종류가 있기 때문에 우선적으로 평면의 제약을 가해서 접근하기 쉬운 평면들로부터 보통 연구를 시작한다. 그래서 많이 관심을 갖는 평면은 원뿔 모양, 원통 모양, 포물선 모양의 회전체 등의 겉넓이다. 이러한 평면에 관해서 제한문제들도 많이 알려져 있고, 또한 많은 부분이 풀려 있다.

지금까지 조화해석학에서 글쓴이의 연구 분야에 대해 이야기했다. 이런 문제들이 어디에 응용이 되는지 궁금해 하는 사람들이 있을 수 있다. 글쓴이 역시 궁금했고, 다루지는 않았지만 조화해석학에서 많이 다루는 라돈(Radon) 변환은 단층촬영 즉 X-레이와 관련된 많은 부분에서 사용되고 있다. 물론 순수수학을 전공으로 하면 실생활과는 동떨어진 문제를 자주 접하게 된다. 왜냐하면 문제를 응용하다보면 더 고차원에서 문제를 다루기도 하고, 더 일반화시켜서 접근을 하기 때문이다. 물론 수학을 전공으로 연구하는 사람들은 새로운 문제와 그 해결방법에 대해 고민하는 즐거움이 있지만, 수학이 전공이 아닌 사람들이 보기에는 이해하기 어렵고 접근하기 어려운 점도 있다. 이 차이를 줄이기 위해 수학이 전공이 아닌 사람들도 쉽게 이해할 수 있게 설명이 되는 것이 중요하다고 생각한다.