필자의 연구 분야는 수학에서 편미분방정식이라고 하는 것인데, 자연현상과 생명현상 나아가 심리학과 경제학 등 다양한 다른 분야에 적용될 수 있는 수학분야라고 볼 수 있다. 요즈음의 과학 및 연구 동향이 학제 간 연구인데, 이러한 맥락에서 볼 때에도 수학과 편미분방정식은 다른 분야에 응용성이 높은 분야로 알려져 있다. 특히 필자의 연구 주제는 이런 동향이 반영되어 편미분 방정식 이론들을 물리겭薰컖천문학 등의 분야에서 제기되는 문제들에 응용하는 것이다. 크게 연구 분야를 나누어 본다면 △수리생물(Mathematical Biology) △Application of Kinetic Equations in Physics △Hydrodynamic Stability이다.

먼저 수리생물은 수리물리에 비하면 그 역사가 짧은 분야이기 때문에 연구가능성이 넓고 크다고 볼 수 있다. 1963년 노벨상을 수상한 Hodgkin과 Huxley는 Squid의 Axon Membrane에서 나타난 전기적 흥분 현상인 Excitability를 Hodgkin-Huxley 모델이라는 수학적인 미분방정식으로 설명하여, 중요한 생리현상을 밝혀내는 데 있어 수학적인 방법을 도입하여 성공한 사례를 남겼다. 이는 18~19세기에 출발한 전기생리학(Electrophysiology)에 큰 진보와 함께 학제 간 연구가 생물학에서도 중요하게 대두되는 계기가 되었다. 한편 21세기 생물학에 있어 중요한 분야 중 하나인 분자(Molecular Biology) 및 유전생물학에도 수학 물리와 같은 학제 간 연구가 활발히 전개되고 있다. 이러한 동향에 맞추어 암이나 당뇨병과 같은 현대병을 연구하는 데에도 수학이나 물리 등의 방법들이 사용되고 있다. 21세기의 연구는 학제 간 연구가 대세라고 하는 과학자들의 발언이 과언이 아닌 것이다.

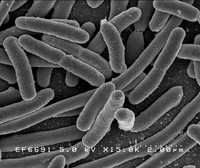
필자는 특히 Chemotaxis라고 하는 세포 간에 일어나는 현상을 연구하고 있는데, 이것은 아메바나 박테리아*종양세포 간에서도 일어나는 군집(Aggregation) 현상이다. 예를 들어 Dicty(Dictyostelium Discoideum)이라고 하는 Cellular Slime Mold 아메바와 Escherichia Coli라고 하는 박테리아는 평상시 랜덤하게 움직이다가(사진) 주된 Carbon Source가 심하게 부족하게 될 때 자신들이 만들어 내는 특정의 화학물질을 섭취하게 되는데, 이러한 Metabolism에 일어나는 현상 중 하나를 Chemotaxis라고 한다. Chemotaxis는 그리스용어로서 Chemo와 Taxis가 결합된 것인데, Taxis는 Directed Movement이고 Chemo는 Chemical의 줄임말이므로 결국 Chemotaxis란 특정 Chemical에 향한 Directed Movement를 의미하는 것이다. 따라서 앞서 말한 아메바 세포들이 Cyclic AMP(cAMP) 라는 특정 화학물질을 만들어 내고, 이 cAMP가 External Signal이 되어 Dicty라는 아메바가 군집하는 현상이 Chemotaxis의 한 예가 될 수 있다.

이러한 군집현상을 이해하는 데 있어 수학적인 다양한 방법들이 접근되고 있다. 아메바 등에 일어나는 Chemotaxis 현상을 기술하는 Keller-Segel 모델이라고 하는 편미분 방정식이 있는데, 이것은 단위당 아메바 세포 수와 cAMP의 분포함수의 시간 변화를 모델로 한 것이다. 이 Keller-Segel 시스템은 군집현상을 예측하는 데 좋은 모델이며, 또한 화학물질에 유도된 세포들의 움직임 중의 하나인 Travelling Wave를 설명하는 데에도 사용되고 있다.
지금까지 아메바나 박테리아 등의 무리 혹은 집단으로서의 행동(Population-level) 등에 관한 것이라면 박테리아세포 하나하나의 행동(individual-level)과 그 둘의 관계 즉 개인에서 집단으로의 관계는 또다른 문제가 될 수 있는데, Chemotaxis와 관련하여 필자가 관심 갖고 있는 문제 중 하나라고 볼 수 있다. 특히 하나의 박테리아 움직임을 실험한 데이터를 보면 그것은 한동안 거의 일직선으로 움직이다가(Run-평균 1초), 어느 순간 화학물질에 유도되어 방향을 바꾸고(Tumble-평균 1/10초), 다시 다른 일직선으로 움직이는 소위 ‘Run and Tumble’을 반복하며 움직인다. 이런 세포 하나의 움직임은 연속적이지 않은 Stochastic Process인 Velocity Jump Process를 보이므로, 기존의 Keller-Segel(Macroscopic 모델)로는 세포 하나의 움직임을 기술하기가 어려워지므로, 보다 Microscopic 모델을 필요하게 되고 1980년대에 처음으로 모델이 된다.

편미분방정식으로 구성된 Microscopic 모델 자체뿐만 아니라 Microscopic 모델로부터 Macroscopic Model로 유도하는 것 또한 생물학적으로나 수학적으로 중요한 문제가 된다. 이를테면 각각 박테리아의 행동들이 집단행동에 어떤 영향을 미치느냐하는 문제 같은 것이다. 실제 아프리카대륙을 비롯한 많은 나라에서 메뚜기 떼들로 인한 농작피해가 심각한데, 집단으로서 즉 떼로 몰려다니는 메뚜기들의 행동을 각각 메뚜기 행동들로 설명할 수 있는가 하는 문제는 그런 농작물 피해 방지에 단서가 될 수 있을 것이다. 개인에서 단체로의 관계는 비단 생태학에서뿐 아니라 세포 단계에서도, 즉 하나의 세포가 다세포로 이루어진 존재에게 어떤 역할을 하는가에 대한 질문에도 적용되는 것이며, 일반적으로 아주 어렵지만 중요한 문제라고 생각된다.

생물수학에서 필자가 관심 있는 다른 문제는 세포나 동물에 나타나는 패턴형성에 관한 것이다. 예를 들어 얼룩말과 표범에 나타나는 띠무늬나 점박이 무늬 같은 것이 왜, 어떻게 형성되었는지에 대한 문제, 혹은 종양세포조직을 관찰해보면 혈관세포와 같이 네트워크모양이 형성되는데, 이런 것들에 대한 문제이다. 이런 현상 또한 편미분방정식과 그에 따른 분석, 그리고 수치 해석적인 방법들로 접근하여 설명되고 있다.
생물수학 연구에서 항상 주의해야 하는 것은 연구가 실험적인 현상이나 실제현상과 얼마나 연관되어 있는지를 염두에 두고 실제 실험가들이나 의사들과 함께 일하는 것이 중요하다. 사실 실제 생물학적인 시스템은 굉장히 복잡다양하기 때문에 수학적 혹은 물리적 접근이 용이한 것은 아니며, 실질적으로 수학적 방법 도입이 가능하고 의미 있는 부분은 아직 아주 적다. 그렇기 때문에 생물수학이 안고 있고 넘어야 할 과제는 많다. 생물수학이라는 분야가 태어난 지 오래지 않으며, 최근 연구가 홍수 같이 범람하는 추세를 바라볼 때 분야 자체를 잘 정립하는 것과 방향성과 정체성 또한 풀어나가야 하는 숙제라 하겠다.

또 다른 연구주제는 유체나 플라스마에 나타나는 안정성(Stability)과 불안정성(Instability) 현상에 관한 것이다. 자연계를 살펴보면 처음의 작은 변화가 시간이 흐름에 따라 계속 작은 변화로 유지되는, 즉 안정적인 시스템이 있는가 하면 그와 반대로 처음의 작은 변화가 나중에 엄청난 변화를 야기 시키는 시스템도 존재한다. 1940년 11월 7일 미국 워싱턴 주에서 일어난 Tacoma Narrows Bridge(만들어졌을 때 세계에서 3번째로 큰 다리) 붕괴사건은 바람에 유도된 파동 불안정성 현상의 한 예를 보여준다. 이러한 안정성과 불안정성 현상은 전자와 같은 미세한 스케일에서도 나타나고, 크게는 은하계나 Solar Wind 같은 플라스마에서도 나타나는 현상이다. 또 비누 막을 통한 프린터산업이나 효율적인 오일분리를 통한 정유산업 등에도 응용되는 연구라고 볼 수 있다. 실제로 정유산업에 있어서 얼마나 효율적으로 기름을 그 밖의 유체들과 분리하여 얻어낼 수 있는가 하는 문제는 매우 현실적인 문제 중의 하나이며, 이에 동기를 둔 수학적 연구가 Saffman-Talyor Instability라고 한다. 필자는 이러한 다양한 응용문제를 수학적으로 접근하는 연구를 하고 있다.

마지막으로 필자의 또 다른 연구 분야는 좀 더 수학적인 문제로서, 플라스마에서 나타나는 물리적 시스템의 해의 존재성 등에 관한 것이다. 전자총이나 다이오드에 있는 전자 양자들을 기술하는 편미분방정식은 Vlasov-Poisson 방정식이며, 이 방정식의 해의 존재성 등을 연구한다. 한편 우주의 기원에 관련된 빅뱅 이론과 블랙홀과 같은 이슈들은 Vlasov-Einstein 방정식과 연관되며, 이에 관한 연구도 하고 있다.
이상과 같이 짧게나마 필자의 연구에 관해 기술했다. 순수수학이 가지는 가치 자체도 높고 훌륭하지만, 또 다른 한편으로는 수학적인 방법과 도구를 가지고 현장의 과학자들과 손을 잡고 토론하며 보다 현실적이고 실제적인 문제를 풀어나갈 수 있다면 좋지 않을까 생각한다. 물론 여러 가지 현실적인 장벽과 문제들이 있다. 지금까지 학제 간 연구의 역사가 오래 되지 않았고, 다른 분야에 있는 사람들 간의 언어장벽문제 등도 쉬운 문제는 아니다. 하지만 서로 열린 마인드를 가지고 그 간의 틈을 좁혀 가며 노력한다면 우리의 과학계도 그리 어두운 것만은 아닐 것이다.